Operations in Singly Linked List | Pseudo Code for all insertions and deletions operations in SLL

2 years ago

thesanjayasubedi99_a51558tx

4 minutes

Singly Linked List

Each node or cell has one link part that contains the address of next node in that list. The link part of last node contains NULL value which is the indicator of the end of the node. The example is shown in figure below:

Linked List Example

Different Operations in SLL(Singly Linked List)

Insertion: There are basically three operations related to insertion in linked list.
- Insert at the beginning:
  The simple process for inserting node at beginning is that we will first set the reference of existing head node to our current node and then the current node is then set to head. The time complexity for this operation i.e the time complexity to insert a node at the beginning or start will be O(1).
  
  Pseudo Code to insert at beginning:
```
addAtFirst(node)
	node.next = head // set reference of current head
	head = node //set the head to our node
```
- Insert at the end:
  In order to add an element at the end, we must first set the current last node reference to the node we are adding, then set the reference or link of the node we are adding to NULL, and then we must set the last node reference to our node. The time complexity for this operation i.e the time complexity to insert a node at the end will be O(1).
  
  Pseudo Code to insert at end:
```
addAtLast(node)
	last.next = node
	node.next = null
	last = node
```
- Insert at the specific position:
  In order to add an element at specific position, you must follow these three steps in linked list:
  1. Start from head and go just before the position where you want to add that specific node.
  1. Set your node’s reference or link to the next position.
  1. Then, set the previous node’s reference to your current node.
  The time complexity for this operation i.e the time complexity to insert a node at the specific position will be O(n).
  
  Pseudo Code to insert at specific position:
```
addAtSpecificPosition(node, position)
	Node temp = head
	for i=1 to position -1; do
		temp = temp.next
	node.next = temp.next
	temp.next = node
```

Deletion: The three main operations of deletion in Single Linked List are
- Delete at beginning:
  The simple task to delete the node at beginning will be to setting the head to second node. The time complexity for this operation i.e the time complexity to delete a node at the start or beginning position will be O(1).
  
  Pseudo Code:
```
deleteStart()
	head = head.next
	//free() or malloc()
```
- Delete at end: The steps to delete the last node are:
  1. Start from head and go upto second last position.
  1. Set the reference of that second last position to null.
  1. Free up that location
  The time complexity for this operation i.e the time complexity to delete a node at the end or last position will be O(n).
  
  Pseudo Code:
```
deleteEnd()
	Node temp = head
	while temp.next != last
		temp = temp.next
	temp.next = null
	last = temp
	//free() or malloc()
```
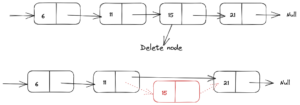
- Delete at specific position: The steps to delete the node at specific position are:
  1. Start from head and go to just before that position.
  1. Set the reference of that position to another next node. If you are at 5th node and you want to delete 6th node then set the reference of 7th node in the 5th node.
  1. Free up that location
  The time complexity for this operation i.e the time complexity to delete a node at specific position will be O(n).
```
deleteSpecificNode(position)
	Node temp = head
	for i=1 to postion -1, do:
		temp = temp.next
	temp.next = temp.next.next
	//free() or malloc()
```
  The visual representation may look like this:
Thanks!

Here are some references that might help you implement Linked List in different programming languages:

Python: Click_Here
Java: Click_Here

I just published another blog article regarding worst case time complexity and bigO notation. You can find out here: Worst Case Complexity .For more DSA Related Topics you can stay tuned here: https://facebook.com/secnep